
ТехнологииФёдоров Александр Александрович: Биография, образование, наука 11:19, 11 Апр. Фёдоров Александр Александрович родился 08.10.1970 в городе Семёнове Нижегородской области. Его родители, журналист и химик, привили ему любовь к зна...
Главные новостиПочтовые ящики жителей Тверской области заваливают анонимной религиозной литературой 11:19, 11 Апр. В последнее время жители Тверской области стали обнаруживать в почтовых ящиках целые подборки буклетов религиозного содержания. В частности, как сооб...
Главные новостиМинистерство финансов инициировало повышение минимальной цены на крепкий алкоголь 11:19, 11 Апр. На портале нормативных правовых актов опубликован проект приказа Минфина, повышающий минимальные цены на крепкий алкоголь. И вроде все правильно, есл...
События и ОбществоУже отпустили? Экс-глава Раменского района активничал в соцсети после ареста за якобы убийство любовницы 11:19, 11 Апр. Проверка на полиграфе косвенно подтвердила вину Андрея Кулакова, сообщают СМИ. После задержания экс-главы Раменского района, на странице подозреваемо...

События и Общество«Почему он не в колонии?»: Известный адвокат возмущена «щадящим» условным сроком для Навального 11:19, 11 Апр. Лидеру ФБК в 2017 году продлили испытательный срок до 2020 года. Адвокат Сталина Гуревич вновь призывает МВД обратить пристальное внимание на персону...

ТехнологииЯндекс представил Алису нового поколения с нейросетевыми функциями 11:19, 11 Апр. Сегодня, 10 апреля, компания Яндекс представила масштабное обновление голосового ассистента Алиса. Новое поколение виртуального помощника работает на...

ТехнологииТоп 8 электрических цепных пил — от проводных до миниатюрных 11:19, 11 Апр. Пилить деревья можно не только ручной или бензиновой пилой, но и электрической. Последние работают тише, меньше вибрируют и не выделяют вредных газов...

ТехнологииНейросеть Apple оказалась круче, чем ChatGPT 4. Ее выпустят вместе с iOS 18 11:19, 11 Апр. Отказавшись от проекта электромобиля, Apple бросила все силы на развитие ИИ и уже добилась определенных успехов на этом поприще. Собственная нейросет...

ТехнологииКитайцы сделали копию AirPods Pro с экраном. Таких наушников нет даже у Apple 11:19, 11 Апр. AirPods Pro с экраном уже стали реальностью, но выпустила из не Apple. Изображение: macrumors.com Уже достаточно давно ходят слухи о том, что Apple с...

Главные новостиРаботников госучреждений заставляют отписаться от Романа Алёхина 11:19, 11 Апр. Интересный приказ пришёл сверху для работников госучреждений и не только. Людей заставляют отписаться от общественного деятеля, социального технолога...

Экономика и ФинансыСильный NFP способен углубить коррекцию в акциях, поддержать доллар 11:19, 11 Апр. Влияние на рынок:2Месячный отчёт по занятости обладает достаточным потенциалом, чтобы рынок определился с тенденцией на ближайшие недели. Но также ес...

Экономика и ФинансыЗолото временно игнорирует негатив 11:19, 11 Апр. Влияние на рынок:3Золото обновляет исторические максимумы почти ежедневно на протяжении последних двух недель, дойдя до $2365 на спот-рынке во вторни...

Главные новостиТест: угадайте советское кино по его названию за рубежом 11:18, 11 Апр. Однако, когда дело доходило до переименования фильмов для иностранных рынков, местные прокатчики часто придумывали собственные названия, порой весьма...

Главные новостиПереживающая всплеск популярности Плетнева рассказала о новом альбоме группы "Винтаж" 11:18, 11 Апр. В апреле группа планирует выпустить новый альбом, который обещает стать настоящим прорывом. Солистка коллектива Анна Плетневой рассказала о новых хит...
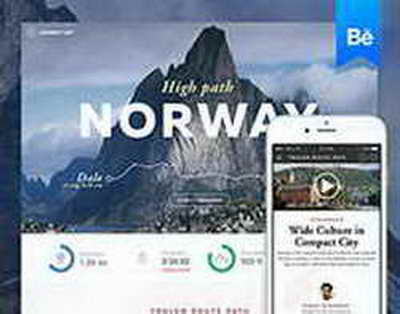
Автомобили и рынкиЭлектрический квадроцикл 11:18, 11 Апр. Электрические квадроциклы - это техника нового времени, которую выбирают из-за экологической безопасности, отсутствия выхлопных газов, относительной ...
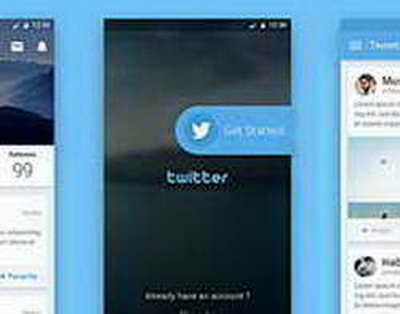
Автомобили и рынкиСумка-холодильник для авто 11:18, 11 Апр. Незаменимый аксессуар для тех, кто любит путешествовать или часто отправляется на дачу. Такое устройство позволяет держать овощи, фрукты свежими, а н...

ЗнаменитостиДжеймс Майкл Тайлер: судьба Гантера из сериала «Друзья» 11:18, 11 Апр. Джеймс Майкл Тайлер – американский телевизионный актёр. Он начинал свою карьеру в Голливуде с низких должностей помощника монтажера и ассистента, одн...

ЗнаменитостиСергей Полунин - российский артист балета 11:18, 11 Апр. Сергей Полунин известен всему миру как гениальный танцовщик с бунтарским характером. У артиста яркая интересная жизнь и непростой творческий путь от ...

ТехнологииКлассическая оптическая нейронная сеть демонстрирует «квантовое ускорение» 11:18, 11 Апр. В последние годы технологии искусственного интеллекта, особенно алгоритмы машинного обучения, добились больших успехов. Эти технологии обеспечили бес...

ТехнологииРазработана водонепроницаемая «электронная перчатка» для дайверов 11:18, 11 Апр. Когда аквалангистам нужно сказать «Я в порядке» или «Акула!» своим партнерам по дайвингу они подают сигналы руками для визуального общения. Но иногда...

Экономика и ФинансыАналитик объяснил, в чем подвох новых вкладов с высокими ставками 11:18, 11 Апр. Банки начали предлагать вклады с плавающей ставкой, которая зависит от ключевой ставки ЦБ РФ. Хотя ставки по ним сейчас высокие, в результате вкладчи...

Экономика и ФинансыНазвана страна с самой щедрой пенсией в мире 11:18, 11 Апр. Пожилые люди в Испании получают самую щедрую пенсию в мире. Выплаты могут доходить до 3060 фунтов стерлингов – 356 000 рублей в месяц, пишет Daily Ma...

ТехнологииПочему входящая скорость интернета низкая / меньше исходящей? 11:18, 11 Апр. По различным причинам входящая скорость мобильного интернета может оказаться ниже, чем исходящая. Расскажем, почему скорость загрузки меньше скорости...

ТехнологииFOSSiBOT F106 PRO — характеристики защищенного смартфона 11:18, 11 Апр. В продажу на AliExpress поступил новый защищенный смартфон FOSSiBOT F106 PRO с большим аккумулятором на 12 000 мАч и хорошей производительностью. Нов...
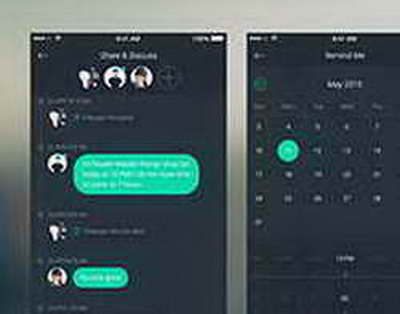
Экономика и ФинансыОбмен Kaspi Bank KZT на карту банка ТКС (Тинькофф) с максимальной выгодой 11:18, 11 Апр. Большинство пользователей, которым нужно провести обмен казахстанских тенге с карты Каспий Банка на рубли карты ТКС Банка, предпочитают пользоваться ...

Экономика и ФинансыКак выбрать правильный участок в Особой Экономической Зоне: Факторы для учета 11:18, 11 Апр. Компания, которая приобретает землю в особой экономической зоне, может получить преимущества. Большим преимуществом можно считать получение налоговых...

Главные новостиВ Самаре устанавливают желтые щиты с символикой дорожного нацпроекта: конструкции информируют горожан о ремонтных работах, запланированных в 2024 году 11:18, 11 Апр. В Самаре своевременно стартовали работы в рамках масштабного ремонта улично-дорожной сети по национальному проекту “Безопасные качественные дороги”. ...

Главные новостиТРИЗ на практике (Теория решения изобретательских задач) 11:18, 11 Апр. ТРИЗ (Теория решения изобретательских задач) – это система методов и приемов, разработанная Генрихом Альтшуллером в середине XX века, с целью с...

Главные новостиЖители Выгоничского района не довольны ситуацией с дорогами 11:18, 11 Апр. С приходом весны, как в Брянске, так и в целом в области ухудшилось состояние дорожной инфраструктуры. В районах области положение хуже, чем в област...

Здоровье и жизньКоролева Рания впервые станет бабушкой: наследный принц Иордании Хусейн и принцесса Раджва ждут ребёнка 11:18, 11 Апр. В королевской семье Иордании радостное событие: наследный принц Хусейн и его жена, принцесса Раджва, которые поженились 10 месяцев назад, в июне прош...

Здоровье и жизнь"Я стала ходячей поучительной историей". Дрю Бэрримор высказалась о зависимости и лечении в рехабе в 13 лет 11:18, 11 Апр. Дрю Бэрримор в интервью журналу People высказалась о борьбе с зависимостями от психоактивных веществ и лечении в рехабе в 13 лет и заявила, что она р...

Главные новостиСмертельно опасная правда: что стоит за чередой инцидентов с самолетами Boeing 11:18, 11 Апр. Один из крупнейших производителей самолетов Boeing испытывает серьезные трудности и находится в эпицентре ряда скандалов. Чрезвычайные ситуации с лай...

Главные новостиНа Пятом канале акция «День добрых дел» для Софьи из Ульяновска 11:18, 11 Апр. ПОЖЕРТВОВАТЬ Сегодня день добрых дел на Пятом канале! И наша помощь нужна 12-летней Софье из Ульяновска. У девочки опасное прогрессирующее заболевани...

Театры и КиноОбщественный деятель Мартыненко Оксана Олеговна 11:18, 11 Апр. Мартыненко Оксана Олеговна является общественным деятелям за которым пристально следит пресса и журналисты. Это неслучайно. Стоит рассказать о личнос...

Театры и КиноКак выбрать песню для игры на пианино: советы и рекомендации 11:18, 11 Апр. Игра на пианино - это не только прекрасное увлечение, но и возможность выразить свои эмоции и чувства через музыку. Однако выбор подходящей песни для...

Бизнес и ПроизводствоЦены на нефть растут на фоне падения запасов нефти в долларах и США 11:18, 11 Апр. Нефть выросла в среду на фоне ослабления доллара, сокращения запасов сырой нефти в США и того, что Великобритания одобрила еще одну вакцину от корона...

Театры и КиноКоролева Рания впервые станет бабушкой: наследный принц Иордании Хусейн и принцесса Раджва ждут ребёнка 11:18, 11 Апр. В королевской семье Иордании радостное событие: наследный принц Хусейн и его жена, принцесса Раджва, которые поженились 10 месяцев назад, в июне прош...

Театры и Кино"Я стала ходячей поучительной историей". Дрю Бэрримор высказалась о зависимости и лечении в рехабе в 13 лет 11:18, 11 Апр. Дрю Бэрримор в интервью журналу People высказалась о борьбе с зависимостями от психоактивных веществ и лечении в рехабе в 13 лет и заявила, что она р...

ТехнологииCS2: борьба за 200 тыс. долларов. Кто победит? 11:18, 11 Апр. В данной статье вы увидите обзор финалистов Elisa Masters Espoо 2023, а также общую информацию по турниру! Турнир Elisa Masters Espoo 2023 – это круп...

ТехнологииValve официально прекратила поддержку CS:GO 11:18, 11 Апр. Компания Valve объявила о прекращении поддержки легендарной игры Counter-Strike: Global Offensive с 1 января 2024 года.С начала нового года компания ...

ТехнологииЧерепно-мозговые травмы меняют нейронные сети по всему мозгу 11:18, 11 Апр. Свежие научные открытия в области черепно-мозговых травм, сделанные американскими нейробиологами из Университета Тафтса в Массачусетсе, раскрывают но...

ТехнологииУчёные выяснили, как отпуск влияет на чувство времени людей и их отношение к работе 11:18, 11 Апр. Из-за пандемии коронавируса множество сотрудников различных британских компаний оказались в ситуации, когда им платили за то, что они не работали. Во...

ТехнологииНаучные исследования подтвердили пользу арт-терапии для психического здоровья 11:18, 11 Апр. В рамках арт-терапии используется искусство (в первую очередь рисование или создание скульптур) для улучшения физического здоровья и эмоционального б...

ТехнологииOCS предлагает сервисы StormWall для защиты от DDoS-рисков и хакерских атак 11:17, 11 Апр. Компания StormWall предлагает рынку решения в области информационной безопасности — сервисы на основе искусственного интеллекта для защиты от DDoS-ат...

ТехнологииIntel демонстрирует сверхбыструю версию Thunderbolt 11:17, 11 Апр. Интерфейс обеспечивает обмен данными с периферийными устройствами на скорости 80 Гбит/с — как только что анонсированная спецификация USB4. Компания I...

Сеть и ИгрыОсновательница магазина корейской косметики рассказала о произволе в Инстаграм 11:17, 11 Апр. Основательница магазина корейской косметики LaskshmiShop рассказала о произволе искуственного интеллекта в ее Инстаграмм аккаунте, на который подписа...

Сеть и ИгрыНасколько корректно бесплатное скачивание музыки в Сети? 11:17, 11 Апр. Давайте в этой статье поговорим о том, насколько корректно скачивать недавно вышедшую в свет музыку в сети Интернет, а также о том, насколько это мож...

Главные новостиВ этом году в Брянске экзамены будут сдавать свыше семи тысяч выпускников 11:17, 11 Апр. В Брянске стартовала экзаменационная пора. Часть выпускников школ уже сдают ЕГЭ. Для них проходит досрочный экзаменационный этап. Всего же продемонст...

Главные новостиВ Брянске готовятся к празднованию 79-летия Победы в Великой Отечественной войне 11:17, 11 Апр. В Брянске на заседании комитета по культуре, спорту и молодежной политике обсудили ход подготовки к празднованию 79-й годовщины Победы в Великой Отеч...

ТехнологииToshiba TV представляет на российском рынке новинки – саундбары Toshiba TS3120A и Toshiba TS5120A 11:17, 11 Апр. Компания Toshiba TV объявляет о поступлении в продажу двух моделей саундбаров – Toshiba TS3120A и Toshiba TS5120A, которые выводят звук на новый уров...

ТехнологииЯндекс представил Алису нового поколения 11:17, 11 Апр. Яндекс представил Алису нового поколения — на основе нейросети YandexGPT. Впервые с виртуальным ассистентом можно будет общаться, как с умным вдумчив...

ЗнаменитостиКоролева Рания впервые станет бабушкой: наследный принц Иордании Хусейн и принцесса Раджва ждут ребёнка 11:17, 11 Апр. В королевской семье Иордании радостное событие: наследный принц Хусейн и его жена, принцесса Раджва, которые поженились 10 месяцев назад, в июне прош...

Знаменитости"Я стала ходячей поучительной историей". Дрю Бэрримор высказалась о зависимости и лечении в рехабе в 13 лет 11:17, 11 Апр. Дрю Бэрримор в интервью журналу People высказалась о борьбе с зависимостями от психоактивных веществ и лечении в рехабе в 13 лет и заявила, что она р...

ТехнологииМеханическое устройство поддержки кровообращения продляет жизнь пациентов с сердечной недостаточностью 11:17, 11 Апр. Та же технология, которая позволяет сверхскоростному поезду двигаться со скоростью до 200 миль в час, не касаясь рельсов, теперь поддерживает учащенн...

ТехнологииРазработана водонепроницаемая «электронная перчатка» для дайверов 11:17, 11 Апр. Когда аквалангистам нужно сказать «Я в порядке» или «Акула!» своим партнерам по дайвингу они подают сигналы руками для визуального общения. Но иногда...

Экономика и ФинансыБесплатный курс по модели Po3 из 5 видео уроков 11:17, 11 Апр. Сегодня представляю вам Бесплатный курс по модели Po3 из 5 видео уроков. Её еще называют: Power of Three / Power of 3 / модель AMD / pattern AMD. Уже...

Экономика и ФинансыВидео курс «Волны Вульфа» — Бесплатно 11:17, 11 Апр. Выкладываю Видео курс «Волны Вульфа» абсолютно Бесплатно! Курс уже очень давно создан, его больше не продаем так же давно, паттерн Волны Ву...
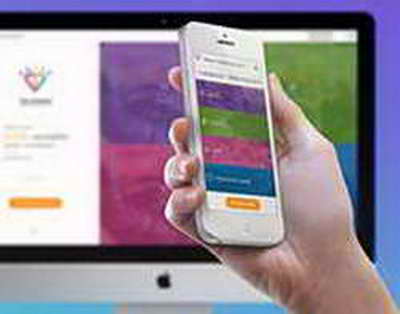
Автомобили и рынкиШины для авто Altra Auto 12:37, 10 Апр. Тип установленных шин напрямую влияет на управляемость вашего авто и его способность к безопасному и эффективному передвижению в любое время года. Гр...

Автомобили и рынкиКалибры и другие инструменты от компании "Микрон" 12:37, 10 Апр. Калибры - это инструменты, предназначенные для контроля размеров и формы деталей, а также для определения наличия и характера дефектов на поверхностя...

ТехнологииТоп 10 - Лучшие проекторы для домашних кинотеатров в жилой комнате 12:37, 10 Апр. Под давлением быстрого снижения цен на телевизоры из обновленной версии обзора полностью исчезли бледные модели проекторов мощностью менее 300 Вт Гла...

ТехнологииТОП 5 - Лучшие LED/LASER проекторы для домашних кинотеатров 12:37, 10 Апр. LED/LASER проекторы пока так и не приблизились по ценам к ламповым моделям, а их уже вытесняют большие телевизоры, которые стремительно дешевеют Наст...

Главные новостиУмер спортивный комментатор Василий Уткин 12:37, 10 Апр. СМИ распространяют информацию о том, что умер спортивный комментатор Василий Уткин. Журналисту было всего 52 года.В последнее время Уткин сильно боле...

Главные новостиКонтртенор Люсьен Сур раскрыл секреты формирования уникального голоса вокалиста 12:37, 10 Апр. Люсьен, как начался Ваш творческий путь? Музыкой я занимаюсь с детства, наверное, лет с 6. Это все мама (улыбается). Она, увидев, мой талант сразу от...

ЗнаменитостиДжеймс Майкл Тайлер: судьба Гантера из сериала «Друзья» 12:37, 10 Апр. Джеймс Майкл Тайлер – американский телевизионный актёр. Он начинал свою карьеру в Голливуде с низких должностей помощника монтажера и ассистента, одн...

ЗнаменитостиСергей Полунин - российский артист балета 12:37, 10 Апр. Сергей Полунин известен всему миру как гениальный танцовщик с бунтарским характером. У артиста яркая интересная жизнь и непростой творческий путь от ...

ТехнологииCS2: борьба за 200 тыс. долларов. Кто победит? 12:37, 10 Апр. В данной статье вы увидите обзор финалистов Elisa Masters Espoо 2023, а также общую информацию по турниру! Турнир Elisa Masters Espoo 2023 – это круп...

ТехнологииValve официально прекратила поддержку CS:GO 12:37, 10 Апр. Компания Valve объявила о прекращении поддержки легендарной игры Counter-Strike: Global Offensive с 1 января 2024 года.С начала нового года компания ...

ТехнологииКак обычный арбуз может довести человека до больничной койки 12:37, 10 Апр. Некоторым людям нельзя есть много арбузов — может потребоваться скорая помощь Арбузы — это вкусные плоды, которые многие из нас в большом количестве ...

ТехнологииЧто такое щекотка и почему мы ее боимся 12:37, 10 Апр. Щекотка — чувство, с которым каждый из нас знаком с детства Чувство щекотки знакомо каждому из нас с детства, однако его сложно описать словами. Оно ...

Спортивные новостиМонте-Карло (ATP). Рублев играет с Попыриным, Хачанов – с Серундоло, Медведев встретится с Монфисом, Синнер – с Кордой, Зверев вышел в 3-й круг, Сафиуллин выбыл 12:37, 10 Апр. Даниил Медведев встретится с Гаэлем Монфисом. Накануне Роман Сафиуллин уступил Новаку Джоковичу. Сетка турнира здесь. Rolex Monte-Carlo Masters Монте...

События странАлександр Назаров и другие члены набсовета НОЦ «Инженерия будущего» выбрали новую рабочую формулу 12:35, 10 Апр. Замглавы корпорации «Ростех» Александр Назаров и другие члены наблюдательного совета НОЦ «Инженерия будущего» приняли новую рабочую формулу. В связи ...

События странШальная стая: бандитский «интернационал» – против России 12:35, 10 Апр. Террористы с Северного Кавказа объединяются под эгидой НАТО То, что определённая часть выходцев с Северного Кавказа обосновалась в странах Европы, пр...
Автомобили и рынкиВ ЛДПР предложили снять плату за проезд по трассе «Дон» для жителей Краснодара 12:35, 10 Апр. Лидер ЛДПР Леонид Слуцкий инициировал разрешение бесплатного проезда по трассе «Дон» для жителей Краснодара. Они поделились проблемой затратной местн...

ТехнологииНеобычные часы SpaceTime Blade измеряют время в километрах 12:35, 10 Апр. Компания Urwerk зарабатывает тем, что выпускает необычные часы. В своей работе она придерживается максимально гибких подходов, а выдумка и оригинальн...

ТехнологииАлло, это кто? Как одно слово может обойтись дорого 12:35, 10 Апр. В современном мире, где технологии играют важную роль в нашей повседневной жизни, мошенники находят новые способы использовать эти инструменты для не...

ТехнологииПочему аккаунт Google пишет «Ограничение по возрасту» и что делать? 12:35, 10 Апр. Некоторые пользователи при регистрации нового аккаунта Google получают уведомление об ограничении по возрасту — в результате создать учетную запись н...

ТехнологииПочему входящая скорость интернета низкая / меньше исходящей? 12:35, 10 Апр. По различным причинам входящая скорость мобильного интернета может оказаться ниже, чем исходящая. Расскажем, почему скорость загрузки меньше скорости...

Здоровье и жизньСпастический запор: Что нужно знать об этом? 12:35, 10 Апр. Спастический запор – это нарушение кишечной активности, характеризующееся чрезмерным напряжением мышц кишечника, что приводит к затруднению прохожден...

Здоровье и жизньДетский мануальный терапевт 12:35, 10 Апр. О мануальной терапии нередко рассказывают чудеса, и это недалеко от истины. Но отличный результат реализуется, если работает хорошо подготовленный сп...

ТехнологииВ Россию привезли Honor Magic 6 Pro 12:35, 10 Апр. Российские ритейлеры анонсировали начало продаж нового флагманского смартфона Honor Magic 6 Pro. На полках он появится только через неделю, пока можн...

ТехнологииКофемашина для офиса: какую выбрать? 12:35, 10 Апр. Кружка ароматного кофе в офисе сделает рабочий день приятнее и эффективнее для большинства сотрудников. Поэтому чтобы они смогли быстро подзарядиться...

ТехнологииЧерепно-мозговые травмы меняют нейронные сети по всему мозгу 12:35, 10 Апр. Свежие научные открытия в области черепно-мозговых травм, сделанные американскими нейробиологами из Университета Тафтса в Массачусетсе, раскрывают но...

Главные новостиВ Брянской области после атак погибли мальчик и женщина 12:35, 10 Апр. Сегодня Брянская область в очередной раз подверглась обстрелу. ВСУ постоянно атакуют регион, и такие новости уже стали привычными, как бы это страшно...

Главные новостиЭксперт Сергей Горелов дал комментарий к 10-летию конфликта в Донбассе 12:35, 10 Апр. В начале апреля 2014 года на востоке Украины начались события, которые положили начало вооруженному конфликту в Донбассе. Этой теме посвящено новое о...

Экономика и ФинансыСильный NFP способен углубить коррекцию в акциях, поддержать доллар 12:35, 10 Апр. Влияние на рынок:2Месячный отчёт по занятости обладает достаточным потенциалом, чтобы рынок определился с тенденцией на ближайшие недели. Но также ес...

Экономика и ФинансыЗолото временно игнорирует негатив 12:35, 10 Апр. Влияние на рынок:3Золото обновляет исторические максимумы почти ежедневно на протяжении последних двух недель, дойдя до $2365 на спот-рынке во вторни...

Главные новости«Ростелеком» в Твери презентовал цифровые сервисы для корпоративных клиентов 12:35, 10 Апр. «Ростелеком» организовал круглый стол для представителей бизнеса и госучреждений Верхневолжья. На мероприятии специалисты провайдера презентовали инт...

Главные новостиВ Тверской области газифицируют музеи 12:35, 10 Апр. 9 апреля под руководством Губернатора Игоря Рудени состоялось заседание Бюджетной комиссии Тверской области. В повестку вошли вопросы поддержки предп...

Главные новостиОткрыта регистрация IV Всероссийского конкурса «Лидеры строительной отрасли» 12:35, 10 Апр. 7 марта на площадке информационного агентства «ТАСС» прошла пресс-конференция официального старта регистрации участников IV Всероссийского конкурса у...

Главные новостиЭксперт Сергей Горелов назвал пять важных для Брянска политических решений 12:34, 10 Апр. Брянск вошёл в ТОП-10 рейтинга Минстрой России по индексу качества городской среды. Участник «Экспертного клуба» из Брянской области Сергей Горелов п...

Главные новостиБрянский эксперт Сергей Горелов назвал спецоперацию ответом на нараставшую десятилетиями агрессию 12:34, 10 Апр. Десять лет назад, 7 апреля 2014 года, в Донецке был создан Республиканский народный совет. Он объявил о суверенитете Донецкой Народной Республики (ДН...

ТехнологииСаундбоксы Vipe Nitro X8 и Vipe Nitro X8 Pulsar: короли твоей вечеринки 12:34, 10 Апр. Vipe, динамично развивающийся бренд аудиоустройств, объявляет о пополнении в серии беспроводных колонок для вечеринок Nitro и представляет две флагма...

ТехнологииToshiba TV представляет на российском рынке новинки – саундбары Toshiba TS3120A и Toshiba TS5120A 12:34, 10 Апр. Компания Toshiba TV объявляет о поступлении в продажу двух моделей саундбаров – Toshiba TS3120A и Toshiba TS5120A, которые выводят звук на новый уров...

Главные новостиОткрыта регистрация IV Всероссийского конкурса «Лидеры строительной отрасли» 12:34, 10 Апр. 7 марта на площадке информационного агентства «ТАСС» прошла пресс-конференция официального старта регистрации участников IV Всероссийского конкурса у...

Главные новостиВ Брянске экзамены будут сдавать свыше семи тысяч выпускников 12:34, 10 Апр. В Брянске началась экзаменационная пора. Часть выпускников школ уже проходят досрочный экзаменационный этап. Всего же к экзамену допущены 7 133 выпус...
Здоровье и жизньЕлизавета Арзамасова и Илья Авербух ждут второго ребёнка 12:34, 10 Апр. 29-летняя актриса Елизавета Арзамасова и 50-летний фигурист Илья Авербух снова станут родителями: супруги ждут второго общего ребёнка. О пополнении в...

Здоровье и жизнь14 вещей в горошек — самого стильного принта этой весны 12:34, 10 Апр. Горошек (polka dot) стал самым модным принтом этой весны, но не каждая готова примерить его. Марк Джейкобс говорил, что "для горошка не бывает неподх...

Закон и ВластьСтрашно жить: В Башкирии орудуют бандиты, выдающие себя за военных 12:33, 10 Апр. Известный в башкирском городе «подполковник» в очередной раз заставил горожан понервничать, рассказывая о своей любви к издевательствам. В Башкирии с...

Закон и ВластьТеневое истребление лесов оставило Сергея Шеверду без отпуска 12:33, 10 Апр. Задержанный министр лесного хозяйства Иркутской области может потянуть за собой и других видных «шишек» городской администрации вплоть до губернатора...

Спортивные новостиНХЛ. «Вашингтон» победил «Детройт», «Рейнджерс» проиграли «Айлендерс», «Филадельфия» пропустила 9 шайб от «Монреаля» 12:33, 10 Апр. «Айлендерс» обыграли «Рейнджерс» (4:2), «Тампа» разобралась с «Коламбусом» (5:2), «Филадельфия» была разгромлена «Монреалем» (3:9). НХЛ Регулярный че...

Спортивные новостиФеерия «Реала» и «Ман Сити», ничья «Арсенала» и «Баварии», камбэк «Автомобилиста», 30-й гол и рекорд Овечкина, новый перл Загитовой и другие новости 12:33, 10 Апр. 1. «Реал Мадрид» и «Манчестер Сити» выдали концерт в Мадриде (3:3) в первом матче 1/4 финала Лиги чемпионов. «Горожане» дважды вели в счете. «Сливочн...

Бизнес и ПроизводствоКак сейчас выглядит киллер, стрелявший во Владислава Листьева 12:33, 10 Апр. Читатели телеграм-канала ВЧК-ОГПУ получили уникальная возможность увидеть, как сейчас выглядят убийцы тележурналиста Владислава Листьева в 1995 году....

Бизнес и ПроизводствоНаместник клана Патрушевых на российском зерне 12:33, 10 Апр. На прошлой неделе Эдуард Зернин, председатель правления Союза экспортеров зерна дал интервью, в котором рассказал, что доля России на мировом рынке з...

Главные новостиКак выбрать сапоги для рыбалки: основные критерии, продукция из магазина Pike 12:33, 10 Апр. Людям, приобщившимся к активным видам отдыха, необходима удобная и ультрапрактичная обувь. При подборе качественной пары сапог для рыбалки важно прин...

Главные новостиПожарная безопасность: подлежащая сертификации продукция, важные услуги 12:33, 10 Апр. В настоящее время вопросы пожарной безопасности занимают особое место в разных отраслях, включая бизнес. Обеспечение пожарной безопасности имеет перв...

Главные новостиНа Михайловском ГОКе приступил к работе новый 70-тонный гусеничный бульдозер 12:33, 10 Апр. На Михайловском ГОКе имени А.В. Варичева — входит в холдинг «Металлоинвест» — ввели в эксплуатацию тяжёлый гусеничный бульдозер. Его вес ...

Экономика и ФинансыБесплатный курс по модели Po3 из 5 видео уроков 12:33, 10 Апр. Сегодня представляю вам Бесплатный курс по модели Po3 из 5 видео уроков. Её еще называют: Power of Three / Power of 3 / модель AMD / pattern AMD. Уже...

Экономика и ФинансыВидео курс «Волны Вульфа» — Бесплатно 12:33, 10 Апр. Выкладываю Видео курс «Волны Вульфа» абсолютно Бесплатно! Курс уже очень давно создан, его больше не продаем так же давно, паттерн Волны Ву...

Автомобили и рынкиШины для авто Altra Auto 12:33, 10 Апр. Тип установленных шин напрямую влияет на управляемость вашего авто и его способность к безопасному и эффективному передвижению в любое время года. Гр...

Автомобили и рынкиКалибры и другие инструменты от компании "Микрон" 12:33, 10 Апр. Калибры - это инструменты, предназначенные для контроля размеров и формы деталей, а также для определения наличия и характера дефектов на поверхностя...

ТехнологииДетский врач рассказала, как безопасно давать ребёнку опиоиды, если их ему прописали 12:33, 10 Апр. Допустим, вашему ребёнку только что сделали операцию. Даже спустя нескольких дней пребывания в больнице боль может оставаться всё ещё очень сильной. ...

ТехнологииЭксперты рассказали, как меняется мозг человека начиная с 30 лет 12:33, 10 Апр. Многие из нас хотят сохранить память и другие мыслительные навыки в старости примерно на том же уровне, что и в молодости. Однако с возрастом память ...

Главные новостиСК закончил расследование убийства ректора махачкалинского религиозного института. Заказчиком назвали бывшего депутата Госдумы Магомеда Гаджиева 12:33, 10 Апр. Следственный комитет назвал заказчиком убийства ректора Института теологии и международных отношений Махачкалы Максуда Садикова, совершенного в 2011 ...

Главные новости«Это все очень, очень плохо». Леонид Волков, просивший снять санкции с руководителей «Альфа-групп», — о решении суда ЕС по делу Фридмана и Авена 12:33, 10 Апр. Леонид Волков, один из ближайших соратников Алексея Навального, раскритиковал решение суда Евросоюза, который решил снять персональные санкции с осно...

ЗнаменитостиСвидетели по делу экс-главы Гагаринского района Романа Журавлева меняют показания 12:32, 10 Апр. Сразу два ключевых свидетеля, которые на этапе следствия изобличали бывшего главу района, на судебном заседании «забыли» о том, как он оказывал на ни...

Знаменитости«Блочные войны» в Колхозном переулке Смоленска: кто прав в «восстании» автовладельцев 12:32, 10 Апр. Бетонные блоки перегораживают проезд в Колхозном переулке в районе домов №№19 и 19а. Smolnarod попытался разобраться в истории соседских «войн&#...

ТехнологииMicrosoft прокачает рейтрейсинг на недорогих видеокартах 12:32, 10 Апр. Microsoft опубликовала патент, который представляет новый подход к сокращению объема памяти, требуемого для обработки графики с использованием технол...

Экономика и ФинансыМаслин Олег: Биография общественного деятеля 12:32, 10 Апр. На протяжении истории человечества всегда находились люди, чьи выдающиеся достижения оказали значительное влияние на различные сферы жизни. Среди них...

Экономика и ФинансыНадёжность сейфов для денег 12:32, 10 Апр. Выбрать надежный сейф для денег бывает затруднительно. Дело в том, что учитывать необходимо сразу несколько ключевых параметров – особенности и тип к...

События и ОбществоПоездка с риском для жизни: смолянин «налетел» на неожиданное препятствие на дороге в центре города 12:32, 10 Апр. Крышка люка, на которую наехал молодой человек, больно ударила не только по авто, но и по бюджету горожанина. Максим, герой нашей истории, — об...

Главные новостиОбщественники и блогеры обсудили перспективы платформы RuTube 12:32, 10 Апр. В студии Экспертного института социальных исследований на международной выставке-форуме «Россия» на ВДНХ состоялась стратегическая сессия с лидерами ...

Главные новостиПолитолог Скачко: Зеленский говорит о новом контрнаступлении ради денег от Запада 12:32, 10 Апр. ВСУ испытывают дефицит живой силы, но для очередной волны мобилизации нужны деньги. Поэтому Зеленский, вновь возвращаясь к теме контрнаступления, пыт...

ТехнологииПроизводство выставочных стендов 12:32, 10 Апр. Изготовление выставочных стендов в Москве сочетает в себе мастерство и современные принципы дизайна, предлагая компаниям уникальную возможность проде...

ТехнологииОптимизация бизнес-операций: Роль драйверов в эффективности работы компьютера 12:32, 10 Апр. В современном бизнес-ландшафте, где скорость и гибкость всех проводимых операций становятся решающими факторами успеха, технологическая эффективность...

Главные новостиКурянам напоминают об опасности сомнительных торговых точек с шаурмой 12:32, 10 Апр. Популярная восточная закуска – шаурма, давно возглавляет хит-парад российского, и не только фаст-фуда. В каждом городе есть, то самое место, с ...

Главные новостиВ Курской области зарплата оказалась ниже средней по нашей стране на 23 процента 12:32, 10 Апр. Накануне один из популярных сервисов по поиску работы, проанализировал доход населения России. Так, в Курской области зарплата ниже средней по стране...
Спортивные новостиТоп-5 самых дорогих футболистов РПЛ составляют игроки «Зенита» 12:32, 10 Апр. Пока элитный футбольный дивизион России – Премьер-лига, находится на зимних каникулах, эксперты футбольного финансового рынка обновили ориентировочну...

Спортивные новостиЭксперты ждут очередного Золотого мяча для Месси 12:32, 10 Апр. После триумфального выступления на футбольном чемпионате мира в Катаре лидер сборной Аргентины Лионель Месси стал основным претендентом на главную ин...

Главные новостиУраган с востока рвет головы. Удар русских ракет поддал Киеву жару и огня 12:32, 10 Апр. Сегодняшний удар по военным объектам Украины был эффективным, точным и беспощадным. В Очакове уничтожена база боевиков ВСУ. В огне и под завалами пог...

Главные новостиОставьте в покое. Шеф Пентагона отчитал Киев за удары по российским НПЗ 12:32, 10 Апр. США опять переживают за российские НПЗ. На этот раз с осуждением ударов по нефтеперерабатывающим заводам выступил шеф Пентагона Ллойд Остин.Приказ из...

Спортивные новостиФеерия «Реала» и «Ман Сити», ничья «Арсенала» и «Баварии», камбэк «Автомобилиста», 30-й гол и рекорд Овечкина, новый перл Загитовой и другие новости 12:32, 10 Апр. 1. «Реал Мадрид» и «Манчестер Сити» выдали концерт в Мадриде (3:3) в первом матче 1/4 финала Лиги чемпионов. «Горожане» дважды вели в счете. «Сливочн...

Театры и КиноОбщественный деятель Мартыненко Оксана Олеговна 12:32, 10 Апр. Мартыненко Оксана Олеговна является общественным деятелям за которым пристально следит пресса и журналисты. Это неслучайно. Стоит рассказать о личнос...

Театры и КиноКак выбрать песню для игры на пианино: советы и рекомендации 12:32, 10 Апр. Игра на пианино - это не только прекрасное увлечение, но и возможность выразить свои эмоции и чувства через музыку. Однако выбор подходящей песни для...

События и ОбществоКак расплачиваться за границей — 6 советов 12:32, 10 Апр. Граждане России столкнулись с трудностями оплаты картами "Мир" в некоторых странах, таких как Армения, Киргизия и Казахстан, из-за введения США санкц...
События и Общество10 секретов выбора идеальной свадебной площадки: как выбрать место проведения свадьбы 12:32, 10 Апр. Во время объявления помолвки многие родственники и знакомые сразу задают вопрос: «Где будет свадьба». Вариантов бесчисленное множество, поэтому важно...

События и ОбществоПопулярные форматы для скачивания музыки и их особенности 12:32, 10 Апр. Возможность загружать и слушать музыку бесплатно в режиме онлайн стала очень популярной в последние годы, и существует множество аудиоформатов, котор...
Читаемое

Знаменитости Сергей Полунин - российский артист балета

Автомобили и рынки Электрический квадроцикл
 Радиальный вентилятор улитка
Радиальный вентилятор улитка


